Optimisation linéaire
Optimisation linéaire
I Programmation linéaire

V Algorithme du simplexe standard
|
Ce cours d'optimisation linéaire est destiné à des étudiants en Mathématiques apliquées ou Informatique, niveau troisième année universitaire. Il est basé essentiellement sur la référence ci-après : {quote} Hédi Nabli, ''Recherche Opérationnelle : Algorithme du Simplexe et ses Applications'', Centre de Publication Universitaire , Tunisie (2006) {quote} Ce livre propose entre autres
Dans ce document, les résultats mathématiques sont donnés sans démonstration. Pour plus de détails, on peut consulter la référence ci-dessus. V Algorithme du simplexe standard VI Dualité en programmation linéaire
Vous trouverez ici une version pdf : docquadratic.pdf Je remercie vivement Sophie Lemaire et Bernadette Perrin-Riou, enseignants-chercheurs à l'université de Paris-Sud, pour leur aide précieuse à réaliser ce document interactif. |
I Programmation linéaire
|
V Algorithme du simplexe standard
| Un programme linéaire est un problème dans lequel on est amené à maximiser (ou minimiser) une application linéaire, appelée fonction d'objectif ou fonction économique , sur un ensemble d'équations et/ou d'inéquations linéaires, dites contraintes . Autrement dit, la programmation linéaire est une branche des mathématiques qui a pour but de résoudre des problèmes d'optimisation linéaire de type Les coefficients et sont des réels fixés et les sont des variables réelles. Les contraintes d'inégalités éventuelles sont toutes larges et non strictes. Il se peut qu'une contrainte d'inégalité soit de type '' 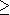 ''. En multipliant chaque inégalité de type '' ''. En multipliant chaque inégalité de type ''
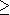 '' par
, on peut supposer que toutes les contraintes d'inégalité
sont de type '' '' par
, on peut supposer que toutes les contraintes d'inégalité
sont de type ''
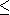 ''. ''.
|
I-1 Généralités
|
V Algorithme du simplexe standard
| Dans le contexte de la programmation linéaire, le terme programmation désigne l'organisation des calculs et non la réalisation d'un programme informatique. Du point de vue des applications, l'optimisation linéaire est d'une grande portée. Elle s'applique à des problèmes très variés qui sont issus de l'économie, de l'ingénierie, de la physique ou encore des modèles probabilistes. Dans ce cadre, on peut citer par exemple, les problèmes de type gestion de stock, gestion de production, transport de marchandise, affectation du personnel, systèmes industriels, réseaux de communication , etc. Pour les modèles de programmation linéaire, on est souvent amené à maximiser un gain ou minimiser un coût. Ceci explique d'ailleurs pourquoi la fonction à maximiser s'appelle fonction d'objectif ou économique. |
|
I-2 Exemple
|
V Algorithme du simplexe standard
|
Exemple
Une usine fabrique deux produits (A) et (B) à
l'aide des matières premières I, II et III. Le fonctionnement
de l'usine est comme suit :
Formulation mathématique
Si on désigne respectivement par
et
les
quantités vendues du produit (A) et (B), le gain total vaut
D'autre part, la disponibilité en matières premières revient à exiger des quantités, utilisées pour la fabrication de et , qui soient inférieures aux quantités disponibles. Ces contraintes s'expriment par les inégalités suivantes : Bien entendu, les variables et doivent être positives. En conclusion, le problème de maximisation du profit se traduit mathématiquement par un programme linéaire qui s'écrit sous la forme :
|
I-1 Généralités
|
I-3 Domaine réalisable
|
V Algorithme du simplexe standard
| Pour un problème d'optimisation linéaire, tout point qui vérifie l'ensemble des contraintes s'appelle point réalisable ou admissible . L'ensemble de tous les points réalisables s'appelle domaine réalisable . Il est facile de vérifier que le domaine réalisable d'un programme linéaire est convexe. On rappelle qu'un ensemble est dit convexe si à chaque fois qu'il contient deux points et , il contient le segment joignant et . Ce segment est souvent noté par et il est défini par Un point est dit optimal s'il est admissible et s'il réalise l'optimum de la fonction d'objectif sur le domaine réalisable. Par exemple, pour le problème tout point réalisable vérifie D'autre part, le point est réalisable et on a . Donc, la solution réalisable est optimale et la valeur maximale de sur le domaine réalisable est . |
I-1 Généralités
|
I-4 Présentation des méthodes
|
V Algorithme du simplexe standard
| Nous allons présenter des techniques qui permettent de résoudre les programmes linéaires que l'on convient désormais de noter (PL). Diverses méthodes ont été proposées dans la littérature :
|
I-1 Généralités
|
II Méthode graphique
I Programmation linéaire

V Algorithme du simplexe standard
| Nous allons décrire la méthode graphique à travers trois exemples représentatifs, ayant chacun deux variables structurelles. Le premier admet une et une seule solution optimale. Le deuxième admet une infinité de solutions optimales. Par contre, le troisième exemple n'admet aucune solution optimale. La résolution d'un (PL) par la méthode graphique se fait selon une démarche commune, celle-ci peut être résumée en quatre directives :
|
II-1 Exemple 1
I Programmation linéaire

V Algorithme du simplexe standard
| Reprenons l'exemple
Le domaine réalisable est schématisé en gris sur la Figure. Toute droite d'équation , où est un réel fixé, est parallèle à la droite : . On constate aussi que tout déplacement parallèle de dans le sens de la flèche (voir dessin ci-après) fait augmenter . Donc maximiser la fonction , tout en satisfaisant aux contraintes du problème, revient à chercher la droite la plus éloignée (dans le sens de la flèche) de et qui coupe le domaine réalisable. Du point de vue graphique, il s'agit de la droite passant par le point et parallèle à . Ainsi, on peut conclure que le point est la seule solution optimale qui donne une valeur maximale de la fonction d'objectif égale à . Autrement dit, le meilleur profit vaut DT obtenu en fabriquant unités du produit (A) et unités du produit (B).
|
|
II-2 Exemple 2
I Programmation linéaire

V Algorithme du simplexe standard
| On considère le (PL) suivant :
Le domaine réalisable est la partie non bornée représentée partiellement en gris sur la Figure. Tout déplacement parallèle de dans le sens de la flèche (voir dessin ci-après) fait augmenter . Donc tout point de la demi-droite est optimal et la valeur maximale de vaut (voir dessin ci-après).
|
II-1 Exemple 1
|
II-3 Exemple 3
I Programmation linéaire

V Algorithme du simplexe standard
| On considère maintenant le (PL) suivant :
Le domaine réalisable associé à ce (PL) est la partie non bornée représentée partiellement en gris dans la Figure. Dans le graphique, on observe que toute droite d'équation , avec , coupe le domaine réalisable. Donc, et par conséquent, le problème n'admet aucune solution optimale (voir dessin ci-dessous).
|
II-1 Exemple 1
|
II-4 Remarque
I Programmation linéaire

V Algorithme du simplexe standard
|
Tous les exemples traités ci-dessus possèdent deux
variables structurelles
et
. Pour des (PL) en dimension
, le raisonnement pour la méthode graphique reste le même.
La seule différence est que l'ensemble des points
vérifiant une contrainte
|
II-1 Exemple 1
|
II-5 Exercice
I Programmation linéaire

V Algorithme du simplexe standard
| ExerciceA venir
|
II-1 Exemple 1
|
III Méthode des sommets
I Programmation linéaire

V Algorithme du simplexe standard
| La méthode des sommets est simple, elle se base sur la résolution des systèmes linéaires de Cramer . Cependant, elle est dans la pratique inexploitable car le nombre de systèmes à résoudre est en général trop important. Néanmoins, la méthode des sommets est d'une utilité incontestable : la recherche de l'optimum éventuel sur tout le domaine réalisable se ramène au calcul de l'optimum de la fonction d'objectif restreinte à un sous ensemble fini. Ce résultat sera l'un des outils clé de la méthode du simplexe . {df} Pour toute contrainte d'inégalité ( resp. contrainte de positivité ) d'un (PL) donné, l'hyperplan associé ( resp. ) s'appelle hyperplan frontière . {df} |
III-1 Résultat préliminaire
I Programmation linéaire

V Algorithme du simplexe standard
| Considérons un (PL) à variables réelles. Un point du domaine réalisable est appelé sommet , s'il existe hyperplans frontières dont l'intersection est réduite à .
Théorème
Soit
une application linéaire et
un polyèdre de
. Si
admet son optimum
global en un point de
, il est
aussi atteint en un sommet de
.
Sans nul doute, l'intérêt de ce théorème est immédiat :
L'optimum (que ce soit maximum ou minimum) d'un
(PL), lorsqu'il existe, peut toujours être réalisé sur un
sommet.
La méthode des sommets pour la résolution d'un (PL), consiste donc à :
Exercice
Application 1 : Problème de trains
Exercice
Application 2 : Production optimale
|
|
III-2 Mise en oeuvre
I Programmation linéaire

V Algorithme du simplexe standard
| Appliquons la méthode des sommets aux trois exemples précédents. Pour l'exemple , les sommets du domaine réalisable sont les points (voir Figure ) La valeur de la fonction d'objectif en chacun de ces sommets est
Il est clair que la plus grande valeur de en ces sommets est atteinte au point et vaut . Pour l'exemple , d'après le graphique, les seuls sommets sont et . De plus, on a ce qui entraîne que est une solution optimale. Concernant l'exemple , les sommets du domaine réalisable sont les points , et . La valeur de en chacun de ces points vaut Cependant, on ne peut affirmer que est une solution optimale, puisqu'on a déjà vu que la fonction d'objectif n'est pas bornée sur son domaine réalisable.
Exercice
Méthode graphique générale
|
III-1 Résultat préliminaire
|
III-3 Champ d'application
I Programmation linéaire

V Algorithme du simplexe standard
| La méthode des sommets peut s'appliquer même pour des (PL) ayant un nombre de variables structurelles strictement supérieur à . Afin de déterminer un sommet, on choisit hyperplans ( étant le nombre de variables) parmi les contraintes du domaine réalisable (y compris les contraintes de positivité : ). On obtient ainsi un système linéaire d'ordre que l'on résoud. Si ce système admet une et une seule solution , on vérifie si satisfait les contraintes restantes. Dans ce cas, est un sommet, sinon le choix considéré de ces équations linéaires ne permet pas d'avoir un sommet et pour ce faire, on effectue un autre choix de hyperplans frontières parmi les contraintes. Dans le but d'obtenir tous les sommets, il va falloir balayer tous les choix possibles dont le nombre est égal à . Chaque choix qui aboutit à un système de Cramer dont la solution est réalisable permet d'obtenir un sommet. Enfin, la solution du problème considéré est obtenue en prenant l'optimum de la fonction d'objectif sur tous les sommets.
Remarque
Dans la pratique, la méthode des sommets est en fait très
coûteuse en temps de calcul. D'une part, la détermination
d'un sommet exige la résolution d'un système linéaire de
Cramer d'ordre
dont la solution doit satisfaire les
contraintes restantes. D'autre part, le nombre
est en
général très important. A titre indicatif, on a
! Par ailleurs, cette méthode n'est
applicable que lorsqu'on
est certain que le (PL) admet une solution optimale, ce
qui est a priori difficile à vérifier.
ExerciceRésolution par la méthode des sommets : A venir
|
III-1 Résultat préliminaire
|
IV Méthode du simplexe
I Programmation linéaire

V Algorithme du simplexe standard
| Dans ce chapitre, nous allons étudier une méthode qui évite de parcourir tous les sommets. Plus précisément, le passage d'un sommet à un autre se fait en améliorant la valeur de la fonction à optimiser. De plus, elle fournit un test qui permet d'affirmer le cas échéant que le problème n'admette pas de solution. Nous verrons que les résultats concernant les problèmes de type maximisation, comparés à ceux relatifs aux problèmes de minimisation, sont très similaires. IV-3 Relation entre la frome canonique et standard |
IV-1 Forme canonique
I Programmation linéaire

V Algorithme du simplexe standard
| On convient de dire qu'un vecteur est inférieur à un vecteur , et on écrit , si pour tout , on a . Ici, le terme désigne la -ième composante du vecteur . Nous mettons en garde sur le fait que la négation de n'est pas . En effet, l'inégalité traduit la propriété pour toute composante . Par contre, la négation de , que l'on convient de noter , exprime que l'inégalité ait lieu pour au moins une composante . {df} Une forme canonique ( resp. forme standard ) est un (PL) où toutes les contraintes sont des inégalités ( resp. égalités) et les variables sont astreintes à être positives. {df}
On a déjà expliqué qu'on
peut supposer et sans perte de généralité, que les
contraintes d'inégalité sont toutes de type ''
où , , matrice et sont fixés. Le vecteur a composantes réelles et désigne l'opérateur transposé. Les inégalités |
IV-3 Relation entre la frome canonique et standard
IV-4 Notion de base réalisable
|
IV-2 Forme standard
I Programmation linéaire

V Algorithme du simplexe standard
| La mise sous forme standard d'un (PL) quelconque consiste à transformer les contraintes d'inégalités (mise à part les contraintes de positivité) en égalité tout en imposant aux variables d'être positives. Pour ce faire, on procède comme suit :
Soit la forme canonique (FC) suivante : sous les contraintes 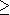
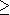
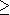 0, 0,
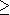 0 0
Les données de la forme standard de cette (FC) sont :
ExempleOn peut dire à juste titre que ce (PL) n'est pas une forme canonique car la première contrainte est une égalité et la troisième variable n'est pas astreinte à être positive. Pour la mise sous forme standard, la première contrainte, qui est déjà une égalité, reste inchangée. Pour la deuxième, on lui retranche une variable positive , elle devient Les variables du (PL) initial s'appellent variables de décision , celles de la forme standard associée s'appellent variables structurelles . |
IV-1 Forme canonique
IV-3 Relation entre la frome canonique et standard
IV-4 Notion de base réalisable
|
IV-3 Relation entre la frome canonique et standard
I Programmation linéaire

V Algorithme du simplexe standard
| L'écriture d'un (PL) sous forme standard est introduite tout simplement parce que l'algorithme du simplexe ne s'applique qu'aux formes standards. En d'autres termes, pour résoudre un (PL) par le simplexe, il faut tout d'abord l'écrire sous forme standard. Etant donné qu'on résoud le (PL) proprement dit et non la forme standard associée, la question naturelle qu'on se pose est de savoir comment retrouver une solution optimale du (PL) de départ à partir d'une solution optimale de sa forme standard . Le théorème suivant établit le lien entre une solution optimale d'un (PL) et celle de sa forme standard, et on se limite au cas où le (PL) considéré est une (FC).
Théorème
est une solution optimale de (FC) si et seulement si
est une solution optimale de la forme
standard associée. De plus, on a
Ce théorème se généralise bien évidemment pour tout (PL) quelque soit son type d'écriture. A titre d'illustration, pour l'Exemple qui n'est pas sous forme canonique, si est une solution optimale de la forme standard associée, compte tenu des variables d'écarts et du changement de variable considérés, on peut dire que est une solution optimale du (PL) initial.
ExerciceForme standard : à venir
|
IV-1 Forme canonique
IV-4 Notion de base réalisable
|
IV-4 Notion de base réalisable
I Programmation linéaire

V Algorithme du simplexe standard
| Désormais, on note tout (PL) écrit sous forme standard par (FS). Par définition, l'écriture matricielle d'un problème (FS) possède la forme suivante : où
sont fixés.
La matrice
contient toujours plus de colonnes que de lignes
(i.e.
) vu que le nombre de variables
structurelles
(variables de décision + variables d'écarts
+ variables dûes aux variables sans restriction
de signe) dépasse le nombre de contraintes
. Sans perte de
généralité, on suppose que la matrice
est de rang
. Sinon,
|
IV-1 Forme canonique
IV-3 Relation entre la frome canonique et standard
|
IV-4-1 Système de base
I Programmation linéaire

V Algorithme du simplexe standard
| Notons par la colonne de . Le vecteur colonne s'écrit alors où est composante de . On appelle système de variables de base tout ensemble de variables distinctes , , prises parmi , telles que le déterminant des vecteurs , est différent de zéro. On rappelle que l'entier désigne le nombre de contraintes d'égalités qui apparaissent dans (FS). La matrice carrée formée par les colonnes , , s'appelle base et les variables , , s'appellent variables hors base . Autrement dit, une base du problème (FS) n'est autre qu'une sous matrice carrée de d'ordre et inversible. Pour mieux visualiser une telle base , on effectue des permutations de colonnes de sorte que la base apparaisse sur les premières colonnes de . Ainsi, on met sous la forme suivante : où et . Les variables , , peuvent aussi être classées selon et : Désormais, l'ensemble des indices de base sera noté par et son complémentaire par . En respectant cette partition, le système vérifie :
Par suite, l'ensemble des solutions dans du système linéaire est égal à Parmi les solutions de ce système, nous distinguons les solutions dites de base pour lesquelles (on écrit à la place de pour dire que les variables hors base sont nulles). Une telle solution existe et elle vaut Noter que toute solution de base réalisable admet composantes nulles relatives aux variables hors base et que les autres composantes vérifient un système de Cramer d'ordre . |
IV-4-2 Optimalité et base réalisable |
IV-4-2 Optimalité et base réalisable
I Programmation linéaire

V Algorithme du simplexe standard
| Par analogie au Théorème , nous allons établir que lorsque (FS) admet une solution, on peut toujours chercher une solution optimale parmi les solutions de base réalisable.
Théorème
Si un problème (FS) admet un optimum global, il existe toujours une
solution optimale qui est une solution de base réalisable.
Remarque
Tout sommet du
domaine réalisable
|
IV-4-1 Système de base
|
IV-4-3 Base dégénérée
I Programmation linéaire

V Algorithme du simplexe standard
| Une solution de base réalisable est dite dégénérée , si en plus des composantes nulles relatives à , il existe une composante du vecteur qui est nulle. Elle est non dégénérée dans le cas où toutes les composantes de sont non nulles et par suite strictement positives. De même, on dit qu'une base réalisable est dégénérée si la solution de base associée est dégénérée. Il est intéressant de noter qu'un point dégénéré est solution de plusieurs bases réalisables. En effet, tout vecteur colonne relatif à une base dégénérée admet au moins une coordonnée , , qui est nulle. En considérant que , on obtient
car Dans la matrice , nous allons remplacer le vecteur colonne par un autre vecteur pour de sorte que la matrice ainsi obtenue soit inversible. Il est clair que est solution du système linéaire , étant donné que |
IV-4-1 Système de base
IV-4-2 Optimalité et base réalisable
|
IV-5 Algorithme du simplexe
I Programmation linéaire

V Algorithme du simplexe standard
| L'algorithme du simplexe est un procédé itératif qui progresse dans un sens évolutif : il passe d'une solution de base réalisable non optimale à une autre solution ayant une meilleure valeur d'objectif. De cette façon, on évite de parcourir toutes les solutions de base réalisable dont le nombre est en général prohibitif. Pour vérifier la non optimalité d'une solution, un simple test sera effectué. De plus, grâce à l'algorithme du simplexe, on sera capable de détecter, le cas échéant, que l'optimum est infini. |
IV-1 Forme canonique
IV-3 Relation entre la frome canonique et standard
IV-4 Notion de base réalisable
|
IV-5-1 Condition d'optimalité
I Programmation linéaire

V Algorithme du simplexe standard
| La fonction d'objectif est entièrement définie par la donnée du vecteur . A chaque base , on note et . D'une façon équivalente, le vecteur (resp. ) s'obtient à partir de en prenant les coordonnée relatives aux variables de base (resp. hors base) associée à la matrice (resp. ). Le classement du vecteur selon et donne . Naturellement, on dit qu'une base est optimale si la solution associée est optimale.
Théorème
On se donne une base réalisable
du problème (FS). Si la
forme standard (FS) est de type maximisation (resp.
minimisation), on considère le vecteur ligne
La condition d'optimalité peut être interprétée comme un test d'arrêt des itérations pour l'algorithme du simplexe. Il reste à décrire la technique qui permet de passer d'une solution de base réalisable non optimale à une autre solution de base réalisable ayant une meilleure valeur économique. Cette partie fera l'objet du paragraphe suivant.
Interprétation
Donner une interprétation économique du
vecteur
. A partir de la solution réalisable
, on construit le point
obtenu en augmentant d'une unité la
-ième variable
hors base. D'après l'égalité
BNyN
, ce point vaut
, où
désigne le
-ième vecteur de la base canonique de
. Si
le point ainsi obtenu est réalisable, on obtient :
Pour un problème de type maximisation, cette dernière égalité s'écrit . Donc, l'élément représente la quantité s'ajoutant à la valeur économique lorsqu'on incrémente d'une unité la coordonnée hors base de , pour autant que le nouveau point obtenu soit réalisable. Semblablement, lorsqu'il s'agit d'un problème de minimisation, correspond à la valeur retranchée de la valeur économique. C'est la raison pour laquelle s'appelle vecteur des coûts réduits (ou coûts fictifs ou encore coûts marginaux ).
ExerciceSommet-Base-Optimalité : A venir
|
IV-5-2 Amélioration de la fonction d'objectif |
IV-5-2 Amélioration de la fonction d'objectif
I Programmation linéaire

V Algorithme du simplexe standard
| On se donne une base réalisable . Le vecteur désigne la colonne de qui est à fortiori une colonne de . On note aussi la colonne d'indice de la matrice . D'ailleurs, n'est autre où est le -ième vecteur de la base canonique de .
Théorème
On suppose que la base réalisable
vérifie
. Il existe donc une composante
du
vecteur
qui est strictement positive. Considérons le
vecteur colonne
de la matrice
. Alors de deux choses l'une
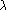 est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie
De plus, on a , selon que (FS) soit de tupe maximisation ou minilisation. Ici, le point représente la solution de base réalisable associée à : .
Il est intéressant de remarquer que dans le cas où la
base réalisable
est non dégénérée, le paramètre
|
IV-5-1 Condition d'optimalité
|
IV-5-3 Algorithme
I Programmation linéaire

V Algorithme du simplexe standard
|
/* On suppose que l'on dispose d'une base réalisable */ while do choisir telle que if then optimum infini /* */ exit else calculer déterminer pour lequel 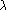 est atteint est atteintend if /* est remplacée par */ /* est remplacée par */ Calculer end while Optimum atteint en et il vaut /* Fin de l'algorithme */ |
IV-5-1 Condition d'optimalité
IV-5-2 Amélioration de la fonction d'objectif
|
IV-5-4 Règle de pivotage
I Programmation linéaire

V Algorithme du simplexe standard
| Dans la pratique, le choix de est souvent multiple, il se peut que plusieurs composantes soient strictement positives. Etant donnée que la nouvelle solution vérifie : il serait commode de choisir la plus grande composante de strictement positive.
Il arrive aussi que le minimum
|
IV-5-1 Condition d'optimalité
IV-5-2 Amélioration de la fonction d'objectif
|
V Algorithme du simplexe standard
I Programmation linéaire

| Dans ce chapitre, les données mise en oeuvre dans l'algorithme du simplexe seront représentées dans un tableau. A chaque itération correspond un tableau appelé tableau simplexe . Des formules itératives liant les éléments d'un tableau au tableau subséquent seront également établies. |
V-1 Tableau simplexe
I Programmation linéaire

| Les éléments qui interviennent dans l'algorithme du simplexe peuvent être récapitulés dans ce qui suit.
Les coordonnées correspondent aux variables de base, et les coordonnées correspondent aux variables hors base. Le terme désigne la valeur de la fonction d'objectif au point réalisable . D'après l'indexation des variables de base, on a :
|
V-3 Sommets et solutions de base V-5 Algorithme du simplexe standard |
V-2 Application
I Programmation linéaire

| Comme application de l'algorithme du simplexe, nous allons résoudre les trois exemples du premier chapitre en utilisant les tableaux simplexe. |
V-1 Tableau simplexe
V-3 Sommets et solutions de base V-5 Algorithme du simplexe standard |
V-2-1 Exemple 1
I Programmation linéaire

| Reprenons l'Exemple 1 :
|
|
V-2-2 Exemple 2
I Programmation linéaire

| Pour l'Exemple 2, le (PL) considéré est
|
V-2-1 Exemple 1
|
V-2-3 Exemple 3
I Programmation linéaire

| Pour l'Exemple 3 :
|
V-2-1 Exemple 1
|
V-3 Sommets et solutions de base
I Programmation linéaire

| Tous les (PL) résolus jusqu'ici sont des formes canoniques puisque le domaine réalisable de chacun peut s'écrire sous la forme Comme conséquence immédiate du Théorème , on peut affirmer que si est une solution d'une base réalisable de , alors est un sommet de . Essayons donc de voir le lien entre les différentes solutions de base réalisable parcourues par l'algorithme du simplexe et les sommets correspondants. Pour l'Exemple , à partir des quatre itérations effectuées, on voit que les sommets de mis en jeu ont été parcourus dans l'ordre suivant : En se référant à la Figure , on remarque que deux sommets relatifs à deux itérations consécutives sont toujours adjacents : ils appartiennent à un même segment de droite frontière de . Cela s'explique algébriquement par le fait que les bases et ne différent que d'une seule colonne. |
V-1 Tableau simplexe
V-5 Algorithme du simplexe standard |
V-4 Formules itératives
I Programmation linéaire

| A chaque itération de l'algorithme du simplexe, on est contraint à calculer la matrice et le vecteur ligne . Ces calculs exigent préalablement la détermination de la matrice inverse . Dans cette section, nous allons voir comment surmonter cette difficulté. Tout simplement, on évitera le calcul de . Les éléments d'un tableau vont être déterminés itérativement à partir des éléments du tableau précédent. |
V-1 Tableau simplexe
V-3 Sommets et solutions de base
V-5 Algorithme du simplexe standard |
V-4-1 Matrice du pivot
I Programmation linéaire

|
Posons
la matrice réelle rectangulaire
avec
. Aussi, on pose
et
où
(resp.
) désigne la
colonne de
(resp.
). Supposons qu'à
l'itération relative à la base
, on ait permuté le vecteur
colonne
avec
. Au niveau du tableau, cela revient à
écrire en gras l'élément
de la matrice
ThéorèmeAfin de mieux visualiser les formules établies dans le Théorème , nous allons illustrer tout d'abord les éléments du tableau simplexe dans le schéma suivant. Le réel { } correspond à l'élément écrit en gras au niveau de la matrice .
Ensuite, le tableau simplexe qui suit sera rempli moyennant des transformations qui peuvent être résumées en ces termes :
|
V-4-2 Vecteur des coûts réduits |
V-4-2 Vecteur des coûts réduits
I Programmation linéaire

| On garde ici le même pivot . Cela veut dire que le vecteur colonne a été échangé par et vice versa. Les formules établies précédemment pour vont conduire aux relations liant les composantes de avec celles de . Pour cela, on pose :
ThéorèmeD'ores et déjà, on peut observer que les relation liant à sont les mêmes que les relations entre une ligne et une ligne en dehors de la ligne du pivot . Le terme , qu'on a convenu d'écrire en gras, se situe sur la même colonne du pivot. Il est remplacé par . Les opérations qu'il faut appliquer sur , , en vue d'obtenir sont identiques à celles effectuées sur les termes de symbole dans le schéma du paragraphe précédent. |
V-4-1 Matrice du pivot
|
V-5 Algorithme du simplexe standard
I Programmation linéaire

| En ce qui concerne le vecteur , il a été indiqué d'avance qu'il peut être déterminé par les relations Si on remplace 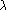 par sa valeur
, on obtient les mêmes formules qui
régissent une colonne de par sa valeur
, on obtient les mêmes formules qui
régissent une colonne de
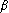 en dehors de la colonne du
pivot. Maintenant, l'élément en bas à droite du tableau simplexe, à
savoir
, se calcule itérativement via la relation
ou
selon que le probème
étudié soit de type maximisation ou minimisation. En tenant
compte de l'expression de en dehors de la colonne du
pivot. Maintenant, l'élément en bas à droite du tableau simplexe, à
savoir
, se calcule itérativement via la relation
ou
selon que le probème
étudié soit de type maximisation ou minimisation. En tenant
compte de l'expression de
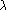 , il est facile de constater que
la formule
s'identifie à la formule
relative à un élément de symbole ''
''. Afin de garder les
mêmes formules, il est souhaitable de remplacer
par
lorsqu'il s'agit d'un probème de type maximisation. Au niveau de
l'implémentation sur machine, il est commode de définir une
matrice, que l'on note
, qui contient les éléments , il est facile de constater que
la formule
s'identifie à la formule
relative à un élément de symbole ''
''. Afin de garder les
mêmes formules, il est souhaitable de remplacer
par
lorsqu'il s'agit d'un probème de type maximisation. Au niveau de
l'implémentation sur machine, il est commode de définir une
matrice, que l'on note
, qui contient les éléments
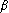 ,
,
et
: ,
,
et
:
La matrice est de taille . D'une itération à une autre, elle est calculée itérativement de la même façon que l'on détermine les éléments symbolisés par '' '', '' '' et '' ''. Afin de balayer tous les paramètres du tableau simplexe, on ajoute à deux vecteurs entiers, notés et et de taille respective et . Pour chaque coordonnée , fournit l'indice de la variable de base du tableau simplexe en cours. De même, correspond à l'indice de la variable hors base. La mise en oeuvre des résultats de ce paragraphe dans l'algorithme du simplexe aboutit à une formulation plus simplifiée au niveau de l'implémentation sur machine. Ici, on suppose que l'on prend systématiquement l'élément le plus élevé. Naturellement, le plus grand parmi les composantes strictement positives est le maximum sur toutes les composantes de .
Algorithme du simplexe standardRequire base réalisable Initialiser , et Calculer while do déterminer l'indice pour lequel le maximum est atteint if then optimum infini /* ou */ exit else calculer déterminer l'indice pour lequel 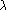 est atteint est atteintend if Calculer end while Optimum vaut Une solution optimale, que l'on note , est donnée par :
Exercice
Résolution par les tableaux simplexe
Méthode du simplexe
|
V-1 Tableau simplexe
V-3 Sommets et solutions de base
|
VI Dualité en programmation linéaire
I Programmation linéaire

V Algorithme du simplexe standard
| Dans le cadre de la programmation linéaire, on peut associer à chaque (PL) un autre (PL), de type opposé, nommé programme dual . Leurs propriétés sont étroitement liées : Par souci d'optimiser les calculs lors de la résolution d'un (PL), il est plus avantageux, dans certaines circonstances, de résoudre le probème dual. Ensuite, la solution du (PL) initial sera déduite facilement par l'intermédiaire de la solution du dual. Une des conséquences les plus fructueuses de la notion de dualité est l'algorithme dual-simplexe qui a été conçu, dans les années , par Lemke. Cet algorithme a un intérêt inéluctable en programmation linéaire. |
VI-1 Primal - Dual
I Programmation linéaire

V Algorithme du simplexe standard
|
VI-2 Optimalité pour le primal-dual |
VI-1-1 Cas d'une forme canonique
I Programmation linéaire

V Algorithme du simplexe standard
| On considère un programme linéaire écrit sous forme canonique que l'on suppose de type maximisation : |
|
VI-1-2 Cas général
I Programmation linéaire

V Algorithme du simplexe standard
| Tout programme linéaire ne s'écrit pas forcément sous forme canonique. Il peut admettre en effet des contraintes d'égalités et/ou des variables sans restriction de signe (s.r.s. en abrégé). De ce fait, la forme générale d'un primal de type maximisation s'écrit de la façon suivante : |
VI-1-1 Cas d'une forme canonique
|
VI-1-3 Tableau récapitulatif
I Programmation linéaire

V Algorithme du simplexe standard
| On note que lorsque le primal est écrit sous une forme générale, son dual l'est aussi. Le tableau ci-dessous récapitule les règles de correspondance entre un primal de type maximisation et son dual.
Remarque
On aurait pu choisir comme primal un
probème de minimisation, le dual aurait été alors un
programme linéaire de type maximisation. Tout simplement parce que le dual du dual
est le primal (facile à prouver).
Autrement dit, si on permutait dans le tableau
précédent les deux mots Primal et Dual , on obtiendrait les règles
de correspondance entre un primal de minimisation et son dual.
|
VI-1-1 Cas d'une forme canonique
|
VI-2 Optimalité pour le primal-dual
I Programmation linéaire

V Algorithme du simplexe standard
|
Théorème
Si
et
sont deux solutions réalisables de
et
respectivement, alors
.
Si de plus on a
, alors
et
sont
deux solutions optimales de
et
respectivement.
Dans la pratique, il est souvent difficile de trouver deux points réalisables et de et tels que . La situation la plus envisageable consiste à déterminer une solution optimale du primal via par exemple le simplexe, puis essayer d'en dégager une solution optimale du dual.
Théorème
Soit
une base réalisable de la forme standard
relative au primal
. Si la base
vérifie
, alors
est une solution optimale du dual
.
Remarque
Afin de déterminer la solution optimale
,
il est inutile de calculer la matrice inverse
. Il suffit, en effet, de résoudre le système de
Cramer
. Par ailleurs, le Théorème
précédent n'exige aucune condition sur la nature du primal (
ou
).
|
VI-1 Primal - Dual

|

