OEF Groupes opérant sur un ensemble
--- Introduction ---
Ce module regroupe pour l'instant 10 exercices sur les
groupes opérant sur un ensemble.
Groupe du carré
On dispose l'ensemble
des entiers entre 1 et dans un carré :
On fait agir le groupe de symétrie du carré
sur
à travers le carré. Donner l'orbite de .
Ecrire l'équation des classes de cette action en donnant (en ordre croissant et avec répétition s nécessaire) les cardinaux des orbites.
Formules des classes I
Un groupe
d'ordre opère sur un ensemble
de cardinal . Pour cette action, il y a orbites. On cherche la liste des cardinaux des orbites.
Combien y a-t-il de possibilités ?
Il y a en effet
possibilités.
possibilité.
Il y a en fait
possibilités.
possibilité.
Donner
pour chacune d'elles
la liste des cardinaux des orbites (séparés par des virgules) :
Formules des classes II
Un groupe
d'ordre opère sur un ensemble
de cardinal . Pour cette action, il y a orbites. On cherche la liste des ordres des stabilisateurs associés aux orbites.
Combien y a-t-il de possibilités ?
Il y a en effet
possibilités.
possibilité.
Il y a en fait
possibilités.
possibilité.
Donner
pour chacune d'elles
la liste des ordres des stabilisateurs associés aux orbites (séparés par des virgules) :
Formules des classes III
Un groupe
d'ordre fini opère sur un ensemble
de cardinal . Pour cette action, la formule des classes est
= Donner l'ordre minimal de
possible ?
Orbites dans Z/nZ
Le groupe multiplicatif
agit sur l'ensemble 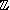 /
/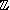 par multiplication
.
par multiplication
. Combien y a-t-il d'orbites pour cette action :
.
Donner les cardinaux de ces orbites dans l'ordre croissant.
.
Questions sur les groupes opérant
-
Groupes opérant et esp. vectoriel
Soit
un corps et
un entier supérieur ou égal à 3. Le groupe
agit
/
sur de l'espace vectoriel
. Sélectionner la bonne réponse.
Opération de groupe
h :
a
a
a
-
Opération transitive
Groupe du triangle
On dispose l'ensemble
des entiers entre 1 et dans un triangle équilatéral : ![]()
On fait agir le groupe de symétrie du triangle équilatéral
sur
à travers le triangle. Donner l'orbite de .
Ecrire l'équation des classes de cette action en donnant les cardinaux des orbites (dans l'ordre croissant et avec répétition si nécessaire).
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les groupes opérant sur un ensemble. interactive exercises, online calculators and plotters, mathematical recreation and games at University of Chieti-Pescara
- Keywords: interactive mathematics, interactive math, server side interactivity, mathematics, abstract_algebra, algebra, group_theory, group_action
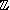 /
/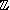 par multiplication
par multiplication