Inégalités
Objectifs
Majorer, minorer, encadrer, voici les techniques de base de l'analyse et ce module a pour but de vous entraîner à ces techniques. Il propose aussi une première approche de la définition de la limite.Guide
- Inéquations
- Implication entre inégalités
- Approche de la limite
- Approche graphique
Inéquations
- Encadrements
- Inéquations : Exercices
- Inéquations : Exercices
- Exercices de déduction d'inégalités simples
Encadrements
Cours : La manipulation des inéqualités est l'occasion de nombreuses
erreurs. Ces manipulations s'appuient sur les propriétés de l'ordre de
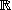 .
.
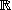 .
.
Exercices : Ces trois exercices proposent d'encadrer des expressions
en
et
connaissant un encadrement des nombres réels
et
.
- Encadrement 1
- Encadrement 2
- Zone d'inégalité
Inéquations : Exercices
Exercice :
Sans étude de fonctions mais en utilisant les propriétés de
l'ordre de
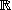 , résoudre les inéquations suivantes :
, résoudre les inéquations suivantes :
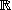 , résoudre les inéquations suivantes :
, résoudre les inéquations suivantes :
-
On pourra s'aider d'un tableau pour enlever les valeurs absolues.S=[-2;5]
-
Attention au signe du dénominateur !Solution -
Attention au signe du dénominateur !Solution,. -
N'oubliez pas la quantité conjuguée !Solution,.
Inéquations : Exercices
Exercices de déduction d'inégalités simples
Les exercices qui suivent demandent de montrer des choses simples mais obligent à décomposer en étapes et à réfléchir à chaque instant aux méthodes que l'on utilise et qui doivent ensuite être utilisées "sans réfléchir". Exercices de déduction (I):
- Fraction simple
- Inverse
Exercices de déduction (II) :
Un pot pourri d'inégalités à résoudre
Exercices de déduction (III) :
Borner une fraction
Implication entre inégalités
Quel est le problème ?
Jusqu'à maintenant, vous avez dû résoudre des inéquations, c'est-à- dire chercher tous les vérifiant une inégalité par exemple : . L'ensemble des solutions est .Dorénavant, vous allez devoir vérifier qu'une condition sur est suffisante pour obtenir un certain encadrement d'une fonction, par exemple : L'implication suivante est-elle vraie ?
Quelles sont les méthodes ?
Considérons une fonction numérique d'une variable , par exempleQue peut-on dire des variations de si varie dans un intervalle donné par exemple [1;3] ? On peut évidemment faire une étude complète de la fonction mais souvent une estimation suffit.
Dans notre exemple, se présente comme une fraction : pour majorer , nous allons
-
majorer le numérateur
La manière la plus simple de majorer est d'utiliser l'inégalité triangulaire : le numérateur est alors majoré par , (pour tout négatif, est compris entre 0 et 1).
On peut aussi travailler un peu plus et remarquer que si est dans [1;3], alors est compris entre 3 et 15 donc est compris entre -6 et +6) et le numérateur est majoré par 6. La majoration est meilleure mais nous avons dû travailler un peu plus. -
minorer le dénominateur
Sur l'intervalle [1;3]
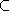 [0;
[0; ], la fonction
sinus est positive donc
est compris entre 0 et
3 et le dénominateur qui vaut alors
est minoré par 4-3=1.
], la fonction
sinus est positive donc
est compris entre 0 et
3 et le dénominateur qui vaut alors
est minoré par 4-3=1.
En conclusion, sur [1;3], on peut dire que la fonction est majorée par 24 et même par 6 si on a été plus courageux.
Exercices
Exercice :
Démontrer les implications suivantes :
-
SolutionPar hypothèse le réel est dans l'intervalle [0;2], l'inégalité triangulaire nous permet de majorer le numérateur :
D'autre part le dénominateur vaut dans l'intervalle considéré donc est minoré par 2.
SolutionQuand est positif, exp est positif et majoré par 1. Quand est supérieur à 16 alors est strictement positif et minoré par . On obtient donc
SolutionPar hypothèse, est compris entre et donc est positif et minoré par (la fonction cosinus est paire de plus elle est décroissante entre 0 et 1) alors que est minoré par . On obtient donc
Approche de la limite
Approche de la définition de la limite
Question :
Dans quel intervalle autour de
puis-je remplacer
par
sans commettre une erreur supérieure à
 ?
Par exemple, dans quel voisinage de
, est-on sûr de
pouvoir remplacer
par 2
en commettant une
erreur
?
Par exemple, dans quel voisinage de
, est-on sûr de
pouvoir remplacer
par 2
en commettant une
erreur
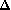 inférieure à
?
inférieure à
?
 ?
Par exemple, dans quel voisinage de
, est-on sûr de
pouvoir remplacer
par 2
en commettant une
erreur
?
Par exemple, dans quel voisinage de
, est-on sûr de
pouvoir remplacer
par 2
en commettant une
erreur
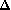 inférieure à
?
inférieure à
?
- On peut s'aider de l' aide graphique par le tracé pour voir ce qui se passe
- Il ne s'agit pas de résoudre une inéquation mais d'appliquer la technique de majoration vue précédemment en faisant intervenir la distance entre et . Il n'est pas important de trouver le meilleur voisinage.
- L'intervalle cherché doit être contenu dans le domaine de définition de la fonction, ici l'intervalle ne doit pas contenir 0. Il est donc contenu dans
Prenons et transformons la différence en valeur absolue de et de :
Maintenant nous allons majorer par une constante sur un intervalle plus petit contenu dans .
Calcul de l'erreur
D'une part est minoré par 1, d'autre part si est supérieur à alors est inférieur à 4, donc pour tout supérieur à ,est majoré par .
Si vérifie , vérifie aussi , La majoration est donc valide et nous avons montré l'implication suivante :
En résumé, si on choisit entre et , on peut dire que vaut 2 à 10-3 près ou que l'erreur est au plus de 10-3.
Le travail central ici est le travail de majoration, en effet ensuite la détermination de l'intervalle est immédiate. Nous pouvons utiliser ce travail de majoration pour affirmer :
Comme notre majoration n'est valide que pour supérieur à , condition qui est vérifiée si appartient à l'intervalle ; on impose la condition . Pour que l'implication soit vraie, il suffit donc de prendre .
Interprétation
Interprétation
L'énoncé mathématique obtenusignifie que
tend vers 2 quand tend vers .
Exercices
Exercice :
Aide visuelle
:
 étant donné,
trouver
étant donné,
trouver
 en étant aidé visuellement.
en étant aidé visuellement.
 étant donné,
trouver
étant donné,
trouver
 en étant aidé visuellement.
en étant aidé visuellement.
Exercice :
Donner une majoration raisonnable de
de la forme
où
est un entier et
un réel positif (on pourra
si nécessaire imposer une condition à
) pour :
-
Solution
Si la condition est vérifiée, on peut donc écrire : -
Solution
Si est compris entre 1/2 et 3/2, (on est alors sûr que la fonction est définie), On minore par (faire un dessin sur la droite réelle en plaçant , , et 2) et on majore par . On peut donc écrire quesi est compris entre 1/2 et 3/2 ,
-
Solution
La fonction est définie seulement si n'est pas nul, nous allons donc prendre compris entre et , alorsest majoré par
Exercice :
Soit
 un réel strictement positif.
Dans chacun des cas traités au-dessus, proposer une valeur de
un réel strictement positif.
Dans chacun des cas traités au-dessus, proposer une valeur de
 dépendant de
dépendant de
 telle que
l'implication suivante soit vraie :
telle que
l'implication suivante soit vraie :
Solution
 sont possibles, le
choix dépend de la majoration qu'on a réussi à faire. Les
majorations proposées permettent d'affirmer que les valeurs de
sont possibles, le
choix dépend de la majoration qu'on a réussi à faire. Les
majorations proposées permettent d'affirmer que les valeurs de
 suivantes conviennent ainsi que toute valeur inférieure.
suivantes conviennent ainsi que toute valeur inférieure.
 un réel strictement positif.
Dans chacun des cas traités au-dessus, proposer une valeur de
un réel strictement positif.
Dans chacun des cas traités au-dessus, proposer une valeur de
 dépendant de
dépendant de
 telle que
l'implication suivante soit vraie :
telle que
l'implication suivante soit vraie :
Solution
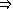
 sont possibles, le
choix dépend de la majoration qu'on a réussi à faire. Les
majorations proposées permettent d'affirmer que les valeurs de
sont possibles, le
choix dépend de la majoration qu'on a réussi à faire. Les
majorations proposées permettent d'affirmer que les valeurs de
 suivantes conviennent ainsi que toute valeur inférieure.
suivantes conviennent ainsi que toute valeur inférieure.
-
. On doit choisir
 inférieur à 1 car la majoration n'est démontrée que pour
.
inférieur à 1 car la majoration n'est démontrée que pour
.
)
-
.
-
.