DOC Etude de signes
Etude de signes
Ce document regroupe les principales techniques d'étude de signes utiles en classe de BTS.
1. Pourquoi a-t-on besoin d'étudier le signe d'une expression ?
2. Signe d'une expression de la forme
3. Signe d'une expression de la forme
4. Signe d'une expression comportant des fractions où figure au dénominateur
5. Signe d'une expression avec la fonction exponentielle
6. Signe d'une expression avec la fonction logarithme népérien
1. Pourquoi a-t-on besoin d'étudier le signe d'une expression ?
- Pour déterminer le sens de variation d'une fonction
, on étudie le signe de sa dérivée :
.
Pour interpréter ce signe :
Si a le signe + sur un intervalle, alors est croissante sur cet intervalle.
Si a le signe - sur un intervalle, alors est décroissante sur cet intervalle. - Pour déterminer la position par rapport à l'axe des abscisses de la courbe représentant une fonction
, on étudie le signe de
Pour interpréter ce signe :
Si a le signe +, alors la courbe de est au dessus de l'axe des abscisses.
Si a le signe -, alors la courbe de est en dessous de l'axe des abscisses. - Pour déterminer la position relative des courbes représentant deux fonctions
et
, on étudie le signe de
Pour interpréter ce signe :
Si a le signe +, alors la courbe de est au dessus de celle de .
Si a le signe -, alors la courbe de est en dessous de celle de .
Exercice QCM
Exercice avec réponses libres
2. Signe d'une expression de la forme ax + b
Autrement dit :
| (*) | |||
| Signe contraire au signe de | 0 | Signe de |
où (*) désigne la solution de l'équation .
Le coefficient de est 3. Il a le signe +.
Le tableau de signes de est donc :
| - | 0 | + |
Exercice
3. Signe d'une expression de la forme ax2 + bx + c
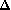 =
.
=
.
- Si
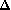 < 0,
ne s'annule jamais et garde toujours le signe de
.
< 0,
ne s'annule jamais et garde toujours le signe de
.
Signe de - Si
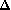 = 0,
s'annule pour une valeur :
et est toujours du signe de
en dehors de cette valeur.
= 0,
s'annule pour une valeur :
et est toujours du signe de
en dehors de cette valeur.
Signe de 0 Signe de - Si
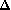 > 0,
s'annule pour deux valeurs de
:
et
.
> 0,
s'annule pour deux valeurs de
:
et
.
est du signe de sauf entre ces deux valeurs.
On note et ces deux valeurs, ordonnées en ordre croissant.Signe de 0 Signe contraire
au signe de0 Signe de
On calcule donc son discriminant :
.
Le signe de est donc toujours le signe du coefficient de , c'est-à-dire le signe +.
| + |
Exemple dans le cas où le discriminant est nul
On calcule donc son discriminant :
.
s'annule pour
Pour tout différent de , le signe de est le signe du coefficient de , c'est-à-dire le signe -.
| - | 0 | - |
Exemple dans le cas où le discriminant est positif
On calcule donc son discriminant :
.
s'annule pour les deux nombres : et
Les deux racines, en ordre croissant sont donc et .
Pour
extérieur à l'intervalle des racines, le signe de
est le signe du coefficient de
, c'est-à-dire le signe -.
Pour
compris entre et , le signe de
est le signe contraire au signe de
, c'est-à-dire +.
| - | 0 | + | 0 | - |
Exercice
4. Signe d'une expression comportant des produits et quotients
- Les règles sont les mêmes pour multiplication et division.
Ceci se fait souvent sous forme de tableau.
On étudie ensuite séparément le signe du numérateur et le signe du dénominateur, puis on utilise la règle des signes, comme précédemment.
= 0 pour
x =
- x + 2 = 0 pour
x =
| x | |||||||
| - | | | - | | | + | |||
| - x + 2 | + | | | - | | | - | ||
| - | || | + | || | - |
Exercice pour revoir la technique de réduction au même dénominateur
Exercice
5. Signe d'une expression avec la fonction exponentielle
- celles qui peuvent se transformer en produit d'une exponentielle par un polynôme,
- celles qui peuvent se mettre sous la forme a ecx + d + b.
Signe du produit d'une exponentielle par un polynôme
Si P(x) est de degré 1 ou 2, on est donc ramené aux cas étudiés dans les § 2 et 3.
Exemples
Pour tout x, on sait que > 0.
Donc a le même signe que .
On doit étudier le signe d'une expression de la forme ax + b. L'équation : = 0 a comme solution x =.
Le tableau de signes de est donc :
| x | |||
| - | 0 | + |
Exercice
Signe d'une expression de la forme a ecx + d + b
- on commence par regarder si le signe est "évident" en tenant compte du fait que l'exponentielle est strictement positive :
4 e3x + 3 et 8 sont donc tous les deux strictement positifs .
4 e() + 8 est la somme de deux nombres strictement positifs .
Cette expression est strictement positive pour toutes les valeurs de x.
| x | |||
| 4 e() + 8 | + |
(*** >0 pour savoir quand *** a le signe + )
La résolution de cette inéquation se fait en "débobinant" la formule construite à partir de x.
on devra alors utiliser les formules valables pour tout
B strictement positif :
On résout l'inéquation : > 0 qui va nous donner l'intervalle dans lequel le signe de sera le signe +.
Attention aux changements de sens des inégalités si on multiplie ou divise par un nombre négatif !
> 0  -3 e-2x -7 > -1
-3 e-2x -7 > -1
 e-2x -7 <
e-2x -7 <
 -2x -7 < ln()
-2x -7 < ln()
 -2x < ln() +7
-2x < ln() +7

Le tableau de signes de est donc :
| x | |||
| - | 0 | + |
Exercice
 ; [.
; [.
 ln(
-5x-3) <
ln(
-5x-3) <
