OEF Dérivation --- Introduction ---

Ce module regroupe pour l'instant 11 exercices sur la dérivation (niveau Lycée, classe de Première, programme 2010).

Dérivée d'une composée de fonction affine

Calculer la dérivée de la fonction , définie sur par   =

NB : Ecrire "sqrt(ax+b)" pour

Dérivée d'une fonction polynôme

Soit la fonction polynôme définie sur RR par .

est dérivable sur RR. Calculer sa fonction dérivée.

Pour tout réel ,   =

Dérivée d'un produit

Calculez la dérivée de la fonction définie sur RR par avec :


Les fonctions et sont dérivables sur et :
=
=

On applique la formule de dérivation :

La dérivée mise sous forme polynomiale développée est :

=

Dérivée d'un quotient

On donne la fonction définie sur RR par   .

Nous allons calculer par étapes :

  • On peut écrire comme un quotient , où les fonctions et sont définies sur RR par :
    =   et  
  • Les fonctions et sont dérivables sur RR :
    =   et  
  • = avec :

      et  

      et  

  • La fonction quotient est dérivable sur
  • On applique la formule de dérivation :
  • est dérivable sur RR .
  • On applique la formule de dérivation :
  • On obtient alors :
    =

Tangente et nombre dérivé

Le plan est rapporté au repère .

La courbe C représente la fonction définie sur .

La droite est la tangente à C au point de coordonnées ( , ).

Sachant que passe aussi par le point de coordonnées ( , ), calculer la valeur de arrondie au dixième.

=
xrange -, yrange -, parallel -,-,-,,1,0, 2*+1, grey parallel -,-,,-,0,1, 2*+1, grey hline 0,0,black vline 0,0,black arrow 0,0,1,0,8, black arrow 0,0,0,1,8, black text black , -0.5,-0.3,small , O text black , 1,-0.3,small , I text black , -0.5,1,small , J text blue , -+0.5 , , medium, y=f(x) linewidth 1.5 plot blue, plot green,

Tangente et nombre dérivé (2)

Le plan est rapporté au repère .

La courbe C représente la fonction définie sur .

La droite est la tangente à C au point de coordonnées ( , ).

On sait de plus que passe aussi par le point de coordonnées ( , ).
Quelle valeur de la fonction dérivée peut-on en déduire ? Donner cette valeur arrondie au dixième.

( ) =
xrange -, yrange -, parallel -,-,-,,1,0, 2*+1, grey parallel -,-,,-,0,1, 2*+1, grey hline 0,0,black vline 0,0,black arrow 0,0,1,0,8, black arrow 0,0,0,1,8, black text black , -0.5,-0.3,small , O text black , 1,-0.3,small , I text black , -0.5,1,small , J text blue , -+0.5 , , medium, y=f(x) linewidth 1.5 plot blue, plot green,

Etude guidée d'un polynôme (deg.3)

Soit la fonction définie par sur l'intervalle [ ; ].
1. Calculer (sous forme développée).

Réponse à la question 1 : Le calcul de dérivée donne : .

Question 2 : On admet que s'écrit sous forme factorisée (produit) comme suit :

Complétez alors le tableau de signes de

| |
0 |
| 0
0 0

Réponse à la question 2 : L'étude de signes de la dérivée donne les résultats consignés dans le tableau ci-dessous.
Question 3 : Complétez ce tableau pour indiquer le sens de variation de la fonction .
(sélectionner une icône dans la liste ci-dessous et la glisser-coller dans une case)

0 0
var. de f

Réponse à la question 3 : Le tableau complet des variations de la fonction est rapporté ci-dessous.

var. de f

Question 4 : D'après ce tableau, le de la fonction est et ce est atteint pour = .

Variation d'un polynôme du second degré

Soit la fonction définie sur 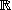RR par   .

Etudier le sens de variation de . Déterminer le(s) extremum(a) de .

  1. La fonction est dérivable sur RR :
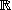    Pour tous réel ,   =
  2. Signe de s'annule en =
  1. Dérivée de
  2. Signe de - + 0
  3. Sens de variation de est strictement sur l'intervalle
  4. est strictement sur l'intervalle
  5. Extremum de atteint en un dont la valeur est
The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.