OEF 梯度
--- 介绍 ---
本模块目前包含 5 个两个变量函数的梯度的练习.
参数曲线与梯度
设
[,] 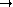 是方程为
其中
是方程为
其中
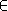 [,] 的
参数曲线.
是从
到
的
函数, 满足
对于
[,] 的
参数曲线.
是从
到
的
函数, 满足
对于
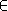 [,].
[,]. 已知以下数据 :
等于多少 ?
在点
的梯度可能不等于零吗 ?
当梯度非零时, 给出
在点
的梯度的斜率的可能值. 如果有多个可能值, 把它们全都写出来 (用逗号分隔).
事实上
在点
的梯度等于零. 我们假设
是
函数. 计算
问
在
是否有局部极值 ?
梯度 I
下图是函数
. 所确定的等距等高线. 计算过
点的等高线在
的的方向 (用斜率表示, 精确到
, 若为无穷大, 则表为 inf).
xrange -, + yrange -, + parallel -,-,+,-,0,/10,20,grey parallel -,-,-,+,/10,0,20,grey arrow 0,0, 0,,10,black arrow 0,0, , 0 ,10,black vline 0,0, black hline 0,0, black levelcurve magenta, , levelcurve blue, , disk ,, 5,blue text black, ,, giant, A
梯度 II
下图是函数
的步长为 的等高线以及两个点
与
. 在
和
两点的
的梯度的模哪一个更些 ?
xrange -, yrange -, parallel -,-,,-, 0,0.5, *20, grey parallel -,-,-,, 0.5,0, *20, grey arrow -,0,,0,10,black arrow 0,-,0,,10,black levelcurve magenta,, disk ,, 5, blue disk ,, 5, blue text black, ,medium, text black, ,medium,
等温线与绝热线
人们把函数
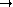 的等值线称为等温线, 而函数
的等值线称为等温线, 而函数
 的等值线则称为绝热线.
的等值线则称为绝热线.
- 点
处于哪一条上? (给出其值)
计算这条曲线在
点的斜率
?
- 点
处于哪一条上 ? (给出其值)
计算这条曲线在
点的斜率
?
-
等于多少 ?
下图画出了
和
的等值线. 是
.
xrange 0,2* yrange -/10,2* levelcurve ,y*x^(), levelcurve ,y*x^(), hline black, 0,0 vline black, 0,0 text black, *1.1,*1.1,medium, A disk ,,7,blue linewidth 2 line -1,-, +1,+, line -1,-, +1,+,
分成几步的练习
斜率与梯度
你现在位于方程为
的山上, 你所处的地图上的位置是 ( , ).
你应该向哪个 (地图上的) 方向前进, 才能最快到达山顶 ? 请在回答中给出
向量 : (
,
)
你的出发方向与成怎样的角度 ? 回答以度为单位, 取最接近的含一位小数的实数.
The most recent version
由于 WIMS 不能识别您的浏览器, 本页不能正常显示.
请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地
使用. 您用自动化程序收集的网页是无用的.
- Description: 一组关于梯度的练习. interactive exercises, online calculators and plotters, mathematical recreation and games at University of Chieti-Pescara
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, gradient, function, slope
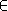 [,]
[,] 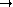 是方程为
是方程为 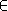 [,]
[,] 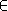 [,].
[,]. 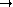
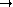 的等值线则称为绝热线.
的等值线则称为绝热线.