 , 用 -inf 代表 -
, 用 -inf 代表 -  ; 如果极限不存在, 则回答 "no".
; 如果极限不存在, 则回答 "no". 还有其它关于定积分应用的模块: OEF 几何积分 以及 OEF 物理积分.
计算函数
你的回答的精度至少是 1/10000.
你的回答的精度至少是 1/10000.
的值是什么 ?
你的回答的精度至少是 1/10000.
.
已知 = . 下面是函数 的图形 :xrange -2, yrange , hline 0,0,black vline 0,0,black line 0,,1,,yellow trange 0, plot black,t, trange -2, line 1,,1,,black dline 1,,1,,black line 0,,0,,black text black,-0.2,-0.2,medium,0 text black,0.6,-0.2,medium,1 gridfill ,*4/5,5,5, gridfill /2,*4/5,5,5, transparent yellow
完成以下结论 :
标出区域的面积代表当 趋于 时 的
标出区域的面积代表当 趋于 时 的
计算当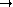 +
+ 与当
与当
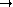 0 时
的极限.
0 时
的极限. 约定 : 输入时用 inf 代表 + , 用 -inf 代表 -
, 用 -inf 代表 -  ; 如果极限不存在, 则回答 "no".
; 如果极限不存在, 则回答 "no".
已知 . 由 定义的函数 的图像如下 :
xrange -0.2,4*pi yrange -*5/4,*5/4 hline 0,0,black vline 0,0,black plot black, gridfill pi/2,*4/5,10,10,blue gridfill 3*pi/2,*4/5,10,10,blue gridfill 5*pi/2,*4/5,10,10,blue gridfill 7*pi/2,*4/5,10,10,blue
计算 .
约定 : 如果极限不存在, 回答 no; 如果极限是无穷大, 回答 inf.
The most recent version请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地 使用. 您用自动化程序收集的网页是无用的.